Back to posts.

Math

Dot product

The dot product supplies as measure of the difference between the direction in which the two vectors point. The dot product of two vectors is given by sum of the products of each component.

How to calculate

A • B  = (A.x * B.x) + (A.y * B.y) + (A.z * B.z)

Angle between vectors

A • B = |A| * |B| cos(rad)
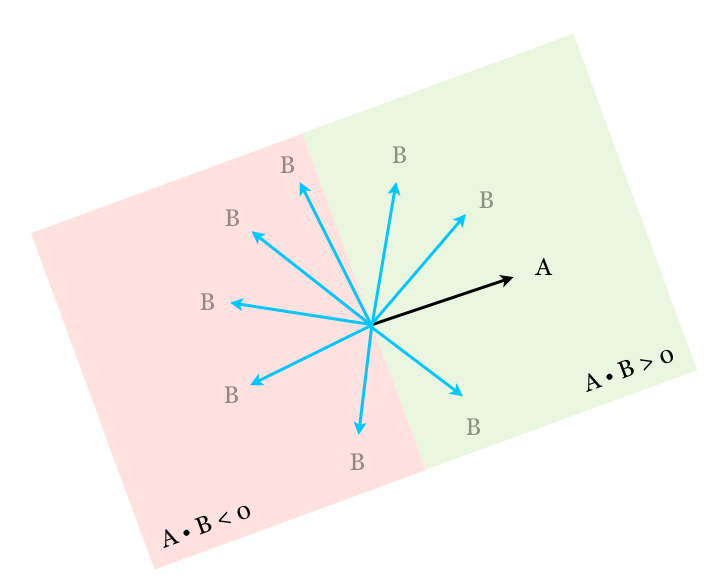
  • A and P are perpendicular when: A • B = 0 (orthogonal)
  • The sign tells us how close the vectors are pointing in the same direction
  • When we consider a plane, passing through the origin and perpendicular to a vector A, then any vector lying on the same side of the plane as A will give a positive dot product, when it's lying on the opposite side, it will give a negative dot product.

Calculating a perpendicular vector based on another one

Sam Hocevar wrote an excellent article on how to get an perpendicular vector based on another one. You can read the article here

// - the current vector does not need to be normalized
// - does not normalize the output
// - works when the vector is non-zero
 
Vec3 orthogonal(Vec3 v) {
 return abs(v.x) > abs(v.z) ? vec3(-v.y, v.x, 0.0)
                            : vec3(0.0, -v.z, v.y);
}

**Convert one range of number to another range*** Lets say you have one range of values between -100 and 300 (A and B), and another range between 400 and 500 (C and D), then you can convert a value (V) from the first range to the second range using:

value = ((V-A) / (B - A)) * (D - C) + C

Rotating, positioning and scaling a 3D model to two 3D points

Lets say you have a 3D model in unit size and two 3D points and you want to position, rotate and scale the 3D model in such a way that it aligns with the vector between the two points. I had to find a solution for this when I had to draw cylinders between two arbitrary points.

I'll describe the solution I used to position, scale, rotate a 3D cylinder with two points. Lets say you have two points A and B. To create a model matrix that will position your model in such a way that it correctly starts drawing at point A and scales length of the cylinder so it touches B, you need to rotate, scale and position. First lets look how to rotate. The model matrix contains all the operations that are needed to draw your 3D model at any position, scale and rotation that you want. The indices of the matrix have a specific meaning:

Assume m is a martrix 4x4, these are the axis of a identity matrix

// The X-axis
m[0] = 1.0;
m[1] = 0.0;
m[2] = 0.0;
 
// The Y-axis
m[4] = 0.0;
m[5] = 1.0; 
m[6] = 0.0;
 
// The Z-axis
m[8] = 0.0;
m[9] = 0.0;
m[10] = 1.0;

The above indices form what I call the Orientation Matrix, also called a LookAt matrix. Basically the values for the separate axis are used to draw those orientation arrows in 3D software:

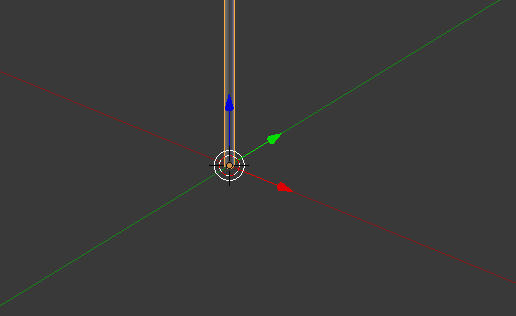
First thing we need to do is decide what axis we want to align with our direction vector. In my case I wanted to align the up vector of my 3D model with the direction vector (B-A), which was the Y-axis. So this simply becomes:

Vec3 y_axis = (b-a);

The next steps are getting the perpendicular axis of this direction vector which will make the X-axis (or z-axis, but those lie in the same plane and are interchangeable in my case). Once we have the y_axis and the x_axis we use the cross product to give us a perpendicular axis of these two. As you might know all the axis of a orientation matrix are perpendicular. So to get all the axis, we use:

Vec3 y_axis = (b-a); // this is the direction vector onto which we want to align the up vector (y-axis) of our model 
Vec3 x_axis = abs(y_axis.x) > abs(y_axis.z) ? Vec3(-y_axis.y, y_axis.x, 0.0) : Vec3(0.0, -y_axis.z, y_axis.y); // this gets us a perpendicular vector of the y-axis, which we call x-axis (we can exchange x-axis <> z-axis here)
Vec3 z_axis = cross(x_axis, y_axis); // we cross the x and y axis to get z-axis.

MAKE SURE TO NORMALIZE THE AXIS! and create the model matrix

When you don't normalize the axis the axis will also have a scaling factor; as I don't want that I'm normalizing them. If you do want to take the scale into account then simply omit the normalize operations. Once we have the 3 axis, we simply fill in our matrix. Indices 12, 13 and 14 are used for the position.

Mat4 m;
m[0]  = x_axis.x;  m[1]  = x_axis.y;  m[2]  = x_axis.z; // x-axis
m[4]  = y_axis.x;  m[5]  = y_axis.y;  m[6]  = y_axis.z; // y-axis
m[8]  = z_axis.x;  m[9]  = z_axis.y;  m[10] = z_axis.z; // z-axis
m[12] = a.x;       m[13] = a.y;       m[14] = a.z;      // a = start position

All code combined (using v1,v2,v3 for the axis)

// v1 = x-axis, v2 = y-axis, v3 = z-axis
Vec3 v2 = (b-a);
Vec3 v1 = abs(v2.x) > abs(v2.z) ? Vec3(-v2.y, v2.x, 0.0) : Vec3(0.0, -v2.z, v2.y);
Vec3 v3 = cross(v1, v2);
 
float len = v2.length(); // scale the Y direction of the cylinder 
 
v1.normalize();
v2.normalize();
v3.normalize();
 
v2 *= len * 0.5;
 
Mat4 m;
m[0]  = v1.x;  m[1]  = v1.y;  m[2]  = v1.z; // x-axis
m[4]  = v2.x;  m[5]  = v2.y;  m[6]  = v2.z; // y-axis
m[8]  = v3.x;  m[9]  = v3.y;  m[10] = v3.z; // z-axis
m[12] = a.x;   m[13] = a.y;   m[14] = a.z;  // position

Step to a certain value

This will step to values of 0.01:

float step = 0.01;
float value = 3.346;
value = floorf( (value/step) + 0.5 ) * step;

References: