Back to posts.

Fast Fourier Transform

For an upcoming project for which we want to use generative audio and audio reactive visuals I'm looking into the Fast Fourier Transform (FFT). I've found the FFT always really interesting although I'm not that math savvy and most articles you read on FFT go really into the maths of how a FFT works.

In this post I won't go into the math of how the FFT works, because other people have a way better understanding of the FFT then I do and they have already written quite good articles on this. See the references below.

You do need to know that the FFT is used to transform a signal from the time domain into the frequency domain. If you're not used to these things this may sound as abacadabra. Fourier describes that any wave is the sum of multiple waves. This article on Better Explained does a good job explaining and visualising this.

I'll limit the rest of this post to the output of a fourier transform as that's what I will be using for this audio reactive system. I'm using the Fastest Fourier Transform in the West library that computes the FFT for us. This library is extremely simple to use and super fast!

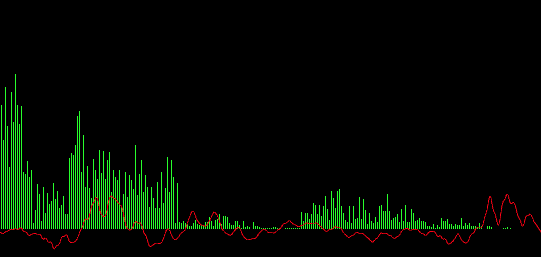
Any FFT function uses input values that it transforms. Because I'm working on an audio reactive system I'm using the audio data as input. In my case I'm giving the fft function 1024 samples (mono) of audio. FFTW has a function which takes doubles as input, so I only need to convert the float values I get in my audio callback function to doubles.

The output of the fft function I'm using, is an array with complex types. This array describes the different sinusoidals of the wave form you passed into the FFT function. Each value from this array is a complex. A complex type has a real and imaginary part. Each of these complex values in the output describes a sinusoidal and how much it contributes to the original wave form.

To use the FFTW library you need to follow a couple of basic steps. First you need to create a plan. A plan is basically a context that is used by the library to make sure the fastest functions are used based on your PC specs. I create a plan where I use "real" values for input and receive "complex" types as output (e.g. r2c) for one dimensional data (the audio). When you create the plan you tell how many elements your input array contains, see the n. You'll also pass in pointer to your input data (in) and to an array that will contain your output data (out). Make sure to use fftw_malloc to allocate the buffers for your input and output data because fftw_malloc will make sure that the memory is correctly aligned for SIMD instructions. Note that I'm using a different size for the output array, see this page for more information on that

int nelements_in = 1024;
int nelements_out = (nelements_in / 2) + 1;
in = (double*) fftw_malloc(sizeof(double) * nelements_in);
out = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * nelements_out);
plan = fftw_plan_dft_r2c_1d(n, in, out, FFTW_MEASURE);

Once you've setup a plan, you can reuse it as many times as you like. Make sure to free the allocated plan and input/output arrays when you don't use them anymore:

fftw_destroy_plan(plan);
fftw_free(in);
fftw_free(out);

To perform the FFT I'm first converting the audio data I get from in my audio callback function to doubles so they can be used by FFTW. Make sure that the number of audio samples you copy to your input array for FFTW has the same size. In my case I'm simply copying the incoming audio data to my input array:

for(int i = 0; i < nframes; ++i) {
    in[i] = data[i * nchannels + 0]; // only using one channel
  }

Once I've converted the audio data, I use the fftw_execute(plan) function to perform the FFT.

fftw_execute(plan);

After calling fftw_execute(plan) you can use the results that are stored in your output variable. Each index describes how much a sinusoidal with a certain frequency contributes to the original wave form and in what way it contributes. You can describe a sinusoidal like: sin(2 * pi * freq + phase ) * amplitude. The magnitude of the complex value represents the amplitude of the wave. The phase is encoded as the angle atan2(imaginary,real).

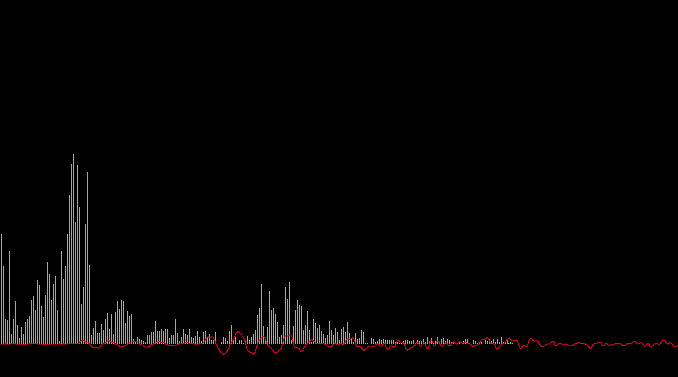
I've been told that a good intuition of the contribution for a particular complex value is the magnitude aka amplitude of the wave. Therefore I'm using sqrtf(imaginary * imaginary + real*real), to get the amplitude. I could use this amplitude/magnitude value as input for my audio reactive visualisation or one can convert it to decibels to get a value which is more representative for the way we perceive audio waves. There is much more to it and I need to do some research on scaling the results into a correct dB range, though the result I get when using 10 * log10f(amplitude) seem correct and are useable.

This is the part where I convert the output array to values I can use:

int extra_scale = 100; // scaling the result a bit    
 
for(int i = 0; i < N/2; ++i) {
  double mag = sqrtf((out[i][0] * out[i][0]) + (out[i][1] * out[i][1])); // out is the output of the fft function
  int value = 10.0f * log10f(mag + 1.0) * extra_scale;  // the + 1.0 is to make sure I don't get negative values, this is the value you should use in your audio reactive system
}

Note: Keep in mind that you don't use all the elements of the output array. We only use (N/2)+1 elements. Also, because the range of frequencies that a human can hear is limited, we don't actually need to process all the results anyway. You can read more about this here

Example

Complete code example (note: I used this code to get into FFT and the FFTW library; please contact me if you see any issues/bugs).

Fourier.h

#ifndef FOURIER_H
#define FOURIER_H
 
#define ROXLU_USE_MATH
#define ROXLU_USE_OPENGL
#include <tinylib.h>
#include <fftw3.h>
 
 
class Fourier {
 
 public:
  Fourier();
  ~Fourier();
 
  void copy(float* data, unsigned int nframes, int nchannels);
 
 public:
  int nelements_in;
  int nelements_out;
  double* in;
  fftw_complex* out;
  fftw_plan plan;
};
#endif

Fourier.cpp

#include "Fourier.h"
#define N 1024
 
Fourier::Fourier() 
  :nelements_in(N)
  ,nelements_out( N / 2 + 1)
{
 
  in = (double*) fftw_malloc(sizeof(double) * nelements_in);
  out = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * nelements_out);
  plan = fftw_plan_dft_r2c_1d(nelements_in, in, out, FFTW_MEASURE); 
}
 
Fourier::~Fourier() {
 
  fftw_destroy_plan(plan);
  fftw_free(in);
  fftw_free(out);
}
 
// copy the raw PCM data to the input buffer for FFTW.  we assume 1024 frames
void Fourier::copy(float* data, unsigned int nframes, int nchannels) {
 
  for(int i = 0; i < nframes; ++i) {
    in[i] = data[i * nchannels + 0]; // only using one channel
  }
}
 
void Fourier::draw() {
 
  fftw_execute(plan);
 
  for(int i = 0; i < (N/2)+1; ++i) {
    double mag = sqrtf((out[i][0] * out[i][0]) + (out[i][1] * out[i][1]));
    int db = (10.0f * log10f(mag + 1.0); 
    int value = db * 100; // scaled the result a bit .. can be used as input for the audio reactive system
  }
}

References